GA-GWNN: Generalized Adaptive Graph Wavelet Neural Network

Abstract

Wavelet-based graph neural networks have received increasing attention in the node classification task. Existing graph wavelet-based approaches, however, are not applicable to arbitrary graphs as they use predefined wavelet filters with built-in homophilic assumptions and disregard heterophily. Recent studies attempted to address this issue through a wavelet lifting transform, which requires a bipartite graph, therefore altering the graph topology and leading to undesirable wavelet filters. This paper proposes a generalized adaptive graph wavelet network that preserves the graph topology through computational trees while implementing the lifting scheme on arbitrary graphs. Moreover, this locally defined lifting scheme integrates both high-pass and low-pass frequency components to further enhance feature representation. Finally, we benchmark our model using nine homophilic and heterophilic datasets, and the results demonstrate the effectiveness of our method.

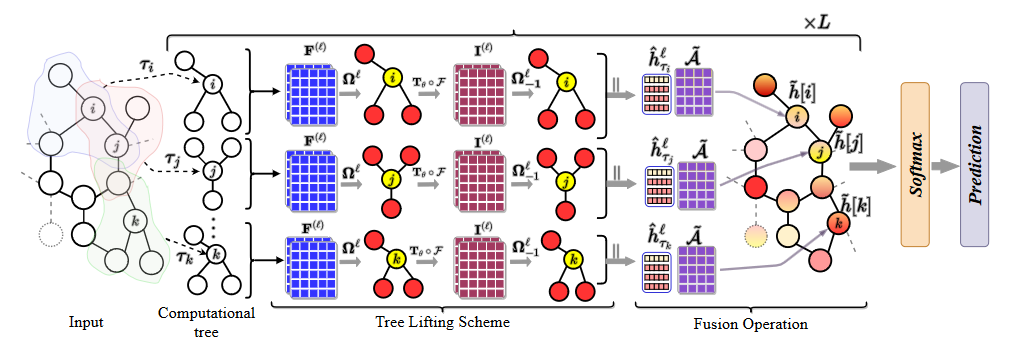
Figure: An overview of the GA-GWNN. The red and yellow colored ball represents nodes with high and low-frequency information respectively, color gradient ball indicates the fusion of both low and high-frequency information, L is the total number of layers. Symbols over the right arrows indicate particular operations.